أثبت عالم الرياضيات هذا نظرية المشي العشوائي لتبرئة اسمه من المتربص

منذ أكثر من 100 عام، وجد عالم الرياضيات المجري جورج بوليا نفسه محاصرًا في حلقة من الإحراج الاجتماعي. كان أستاذًا في المعهد الفيدرالي السويسري للتكنولوجيا في زيوريخ، وكان يستمتع بالنزهات المنفردة عبر الغابة خارج المدينة. وفي إحدى هذه التجوالات مر بجانب أحد طلابه وخطيبته. ثم، في وقت لاحق، وبينما كان لا يزال يتجول بلا هدف، اصطدم بالزوجين مرة أخرى. وبعد ذلك فعل ذلك مرة أخرى.

روت بوليا عن تجربتها في مقال نُشر في كتاب عام 1970، قائلة: “لا أتذكر عدد المرات (التي حدث فيها هذا)، ولكن بالتأكيد كثيرًا جدًا وشعرت بالحرج: بدا الأمر كما لو كنت أتطفل، وهو ما أؤكد لك أنه ليس هو الحال”.

في محاولة يائسة لتبرئة اسمه من المتربص، فعل بوليا ما كان سيفعله أي عالم رياضيات جيد: لقد عمم المشكلة. هل من المقدر رياضيًا أن يتقاطع اثنان من المتجولين؟ لقد بسّطت صياغته الأصلية الصورة من خلال النظر في مشاية واحدة فقط على شبكة لا نهائية. في كل ثانية، يختار المشاة اتجاه البوصلة بشكل عشوائي، بشكل مستقل عن الخطوات السابقة. كان الهدف الرياضي لبوليا هو تحديد احتمالية عودة السائر في النهاية إلى نقطة البداية. تبين أن هذه الإجابة تعادل احتمال أن يلتقي شخصان يمشيان من نفس الموقع مرة أخرى. وجد أنه إذا تجول المشاة إلى الأبد، فإنهم سوف العودة إلى مكان بدايتهم.

حول دعم الصحافة العلمية

إذا كنت تستمتع بهذا المقال، ففكر في دعم صحافتنا الحائزة على جوائز من خلال الاشتراك. من خلال شراء اشتراك، فإنك تساعد على ضمان مستقبل القصص المؤثرة حول الاكتشافات والأفكار التي تشكل عالمنا اليوم.

لم تبرئه الإجابة فحسب، بل كشفت أيضًا عن انقسام أساسي في كيفية تفاعل قوانين الصدفة مع الفضاء المادي. أظهرت حسابات بوليا أنه على سطح ثنائي الأبعاد (مثل أرضية الغابة)، من المقدر للمتجول العشوائي أن يعود إلى نقطة البداية، ولكن في الفضاء ثلاثي الأبعاد، من المرجح ألا يعود هذا الشخص أبدًا إلى نقطة البداية. ينتشر هذا الاكتشاف في مجالات الكيمياء والبيولوجيا، ويشرح أيضًا كيفية عثور جزيئات معينة على المستقبل المناسب على أسطح الخلايا بكفاءة.

كما هو موضح في الطبعة الخامسة لعام 2019 من الاحتمالية: النظرية والأمثلة، بقلم ريك دوريت، قام عالم الرياضيات شيزو كاكوتاني بتجسيد النظرية بطريقة فكاهية: “الرجل المخمور سيجد طريقه إلى المنزل في النهاية، لكن الطائر المخمور قد يضيع إلى الأبد”.

هنا لا يشير مصطلح “الطائر المخمور” إلى صقر طنين، بل يشير إلى عملية عشوائية على شبكة ثلاثية الأبعاد (تخيل صالة ألعاب رياضية في الغابة). وفي كل ثانية يختار الطائر من الشمال والجنوب والشرق والغرب، ومن الأعلى أو الأسفل، بشكل عشوائي، مستقلاً عن الاختيارات السابقة. أثبتت بوليا أنك إذا مشيت عشوائيًا إلى الأبد عبر شبكة مدينة مترامية الأطراف، فلن نضمن لك العودة إلى نقطة البداية فحسب، بل ستصل أيضًا إلى نقطة البداية. كل بقعة على الشبكة عدد لا حصر له من المرات. ومع ذلك، إذا قمت بإجراء نفس العملية في صالة الألعاب الرياضية في الغابة، فسيكون لديك فرصة بنسبة 66 بالمائة تقريبًا لعدم العودة أبدًا إلى نقطة البداية. على نفس المنوال اثنين قد لا يلتقي المتجولون في صالة الألعاب الرياضية في الغابة أبدًا، لكن اثنين من المتجولين على سطح مستو يجب أن يلتقيا عددًا لا حصر له من المرات – لم تكن بوليا تفتقر إلى النعمة الاجتماعية؛ كان يفتقر إلى البعد الثالث للهروب إليه.

وحتى الحالة أحادية البعد، التي تتصرف رياضيًا مثل بعدين، لها آثار في العالم الحقيقي. تخيل أنك تتجه إلى كازينو وفي جيبك 500 دولار. تقدم الطاولة لعبة ذات احتمالات فوز 50-50 (أفضل مما ستجده في مونت كارلو). إذا واصلت اللعب، بغض النظر عن استراتيجية الرهان التي تستخدمها، فسوف تفلس في النهاية. وذلك لأننا نستطيع تمثيل اللعبة على أنها نزهة عشوائية على خط الأعداد. تبدأ عند 500، وبعد كل جولة من اللعب، تتحرك إما يمينًا أو يسارًا على الخط بفرص متساوية. تخبرنا بوليا أنه، كما هو الحال في الحالة ثنائية الأبعاد، إذا لعبت لفترة كافية فسوف تستكشف حتماً خط الأعداد بأكمله. يتضمن هذا 0، وعندها ستفلس. يطلق علماء الرياضيات على هذا اسم “خراب المقامر”، وهو ما يفسر سبب توصيتهم بالتوقف عن اللعب بينما تكون متقدمًا، أو الأفضل من ذلك، عدم اللعب على الإطلاق.

لماذا تغير المسيرات العشوائية الشخصية بشكل حاد بين بعدين وثلاثة أبعاد؟ على الرغم من أن الأبعاد الثلاثة توفر بطبيعة الحال مساحة أكبر للتجول من البعدين، إلا أن هذا وحده لا يكفي كتفسير. ففي نهاية المطاف، يوفر البعدان مساحة أكبر من البعد الواحد، ومع ذلك يظهر كلاهما نفس السلوك.

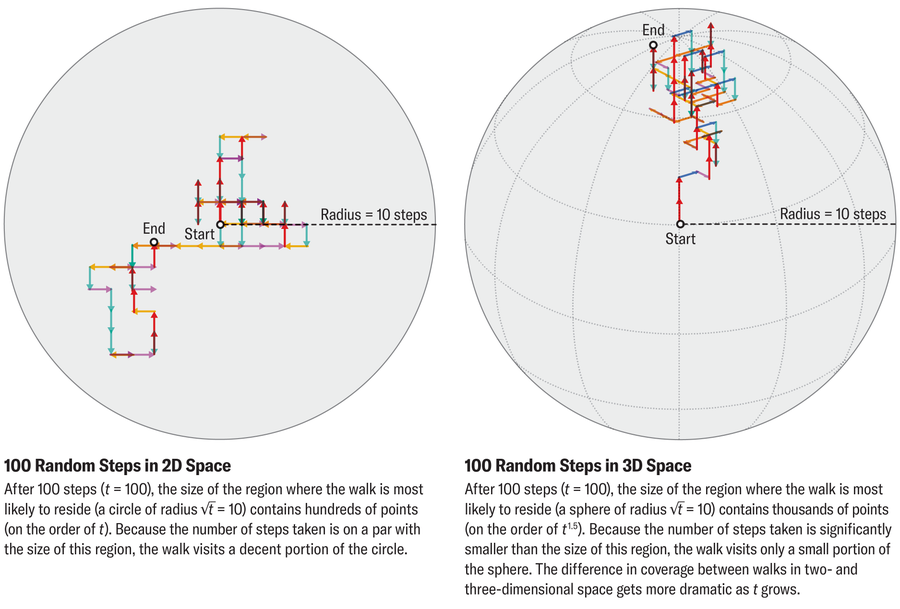
إذا مشيت عشوائيًا لعدد محدود من الخطوات، فسوف نتصل بك ر، فإنك عادةً لن تبتعد أكثر من √ر (الجذر التربيعي لـ ر) بعيدا عن الأصل. بشكل ملموس، بعد 100 خطوة، سيتم العثور على معظم المشاة على بعد 10 خطوات فقط، أو √100، من البداية. بديهيًا، تميل المسيرات العشوائية إلى التحليق بالقرب من نقطة الأصل لأن الخطوات المتعاقبة يمكن أن تلغي بعضها البعض (الماشي الذي يتخذ خطوة باتجاه الشرق تليها خطوة باتجاه الغرب لا يتقدم على الإطلاق). رياضيا، √ر يساوي الانحراف المعياري (مقياس إحصائي لكيفية انتشار مجموعة من القيم) للمسافة من أصل أ ر-خطوة المشي العشوائي.

بمعنى آخر، إذا بدأ العديد من المشاة المنفصلين في نفس المكان ويتجولون بشكل مستقل، فإن مخطط مسافاتهم من نقطة الأصل بعد خطوات t سيبدو مثل منحنى الجرس المتمركز عند 0 ومع الانحراف المعياري √ر. يعد اشتقاق الانحراف المعياري للحالة أحادية البعد تمرينًا سهلاً إذا كنت قد التحقت بفصل دراسي في الإحصاء، فلتجربه.

هذا √ر الرقم موجود في كل البعد وهو المفتاح لفهم نظرية بوليا. فكر في الأمر مثل نصف قطر المنطقة التي سيستكشفها المتجول ر خطوات. نصف القطر هذا له آثار مختلفة تمامًا في الأبعاد المختلفة لأن عدد الأبعاد يحدد ما إذا كنا نتحدث عن الطول أو المساحة أو الحجم. قطعة مستقيمة نصف قطرها √ر له حجم بترتيب √ر; دائرة نصف قطرها √ر له حجم من ترتيب t (مساحة الدائرة تتناسب مع مربع نصف القطر) ؛ وكرة نصف قطرها √ر لديه حجم على ترتيب ر^1.5 (حجم الكرة يتناسب مع نصف القطر المكعب).

ولكن بغض النظر عن البعد، فإن المشاة الذي يتخذ خطوات لا يمكنه زيارة أكثر من ر نقاط متميزة. في أحد الأبعاد، يتجاوز عدد الخطوات حجم المنطقة التي تم استكشافها (ر > √ر)، مما يجبر المشاة على إعادة تتبع خطواته باستمرار. في البعدين، يتطابق عدد الخطوات مع حجم المنطقة (ر = ر) ، مما يسمح للمشاة بتغطية الشبكة في النهاية، وإن كان ذلك بشكل رقيق. لكن في الأبعاد الثلاثة المساحة واسعة مقارنة بعدد الخطوات (ر < ر^1.5)، مع ترك معظم النقاط دون زيارة ومن غير المرجح إعادة النظر في الأصل.

وبطبيعة الحال، نادرا ما يشبه العالم الحقيقي شبكة مثالية، والطيور لا تقلب العملات المعدنية عند كل ضربة جناح. ومع ذلك، فإن هذا التناقض بين المشي ثنائي الأبعاد وثلاثي الأبعاد له فوائد عملية بشكل مدهش في العلوم الطبيعية. أحد الأمثلة المقنعة يتضمن كيفية تفاعل المواد الكيميائية في أجسامنا. غالبًا ما يستخدم الباحثون مسارات عشوائية لنمذجة الجزيئات المنتشرة عبر مادة أخرى. فكر في هرمون يحاول العثور على مستقبل محدد على سطح الخلية. ليس لديها آلية توجيه، لذلك تحدث ردود الفعل هذه من خلال لقاءات الصدفة.

يمكن للهرمون أن يتجول بلا هدف عبر السائل ثلاثي الأبعاد المحيط بالخلية حتى يصطدم بهدفه. وبدلا من ذلك ترتبط العديد من الجزيئات بشكل فضفاض أي نقطة على غشاء الخلية أولا. بمجرد ربطها، تنزلق عبر السطح ثنائي الأبعاد للغشاء حتى تصل إلى هدفها. يؤدي هذا التخفيض في الأبعاد إلى تحويل السير البطيء ثلاثي الأبعاد إلى مسيرة ثنائية الأبعاد فعالة.

في المرة القادمة التي تقابل فيها شخصًا تتجنبه، حاول تحويل اللقاء إلى رؤية رياضية عميقة. من المؤكد أنه يتفوق على الاختباء خلف شجرة.