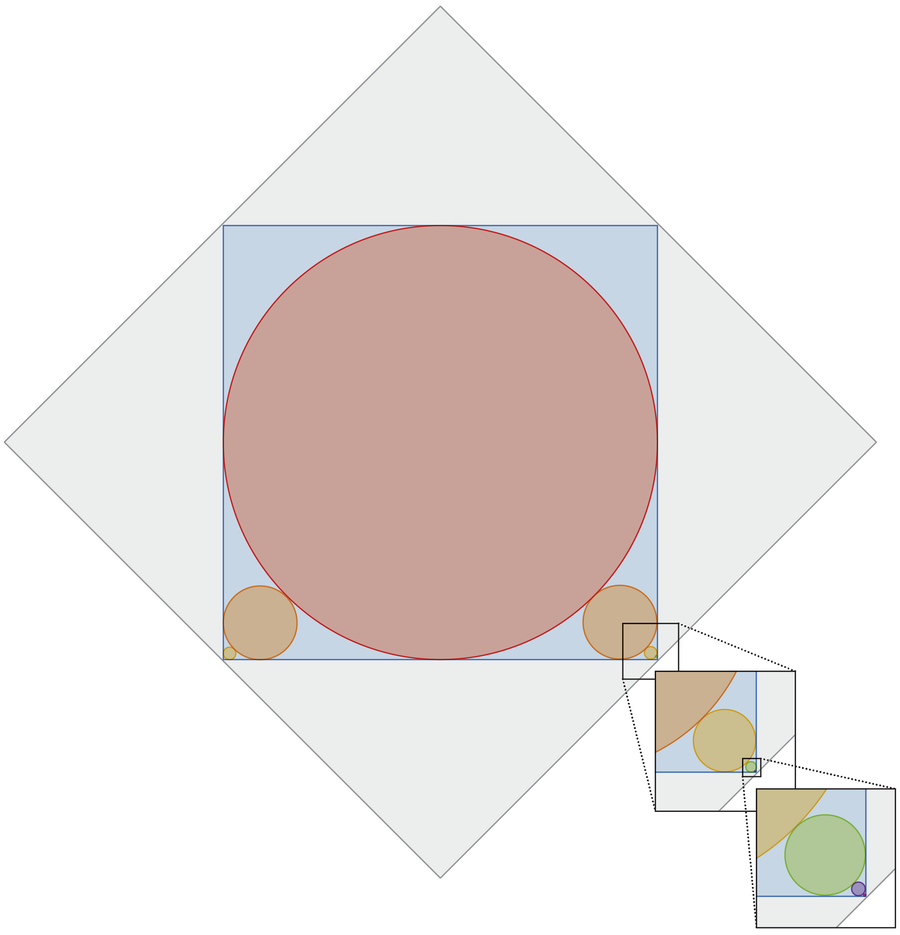
توجد دائرة حمراء داخل مربع أزرق. يترك الترتيب فجوات في أركان المربع الأربعة، اثنتان منها مملوءتان بدوائر أصغر بالكاد تلامس الدائرة الحمراء الكبيرة وجانبي زاوية المربع الأزرق. وهذا بدوره يترك فجوتين أصغر في الزوايا، والتي تمتلئ بدوائر أصغر، وهكذا، مع دوائر أصغر إلى ما لا نهاية. تم إدراج المخطط بالكامل داخل مربع رمادي مقاس 1 × 1. ما هو المحيط الكلي لجميع الدوائر؟
المحيط الكلي لجميع الدوائر هو π. محيط الدائرة يساوي π ضرب قطرها. وبالتالي فإن المحيط الكلي للعديد من الدوائر بأقطارها د1, د2, د3،… يكون:
πد1 + πد2 + πد3 + … = ط(د1 + د2 + د3 + …)
لذا، إذا تمكنا من إيجاد مجموع كل الأقطار، فيمكننا ضرب هذه القيمة بـ π، وبذلك نكون قد انتهينا. وبسبب التماثل فإن أحجام الدوائر لا تتغير إذا قمنا بنقل بعضها إلى زوايا مختلفة:
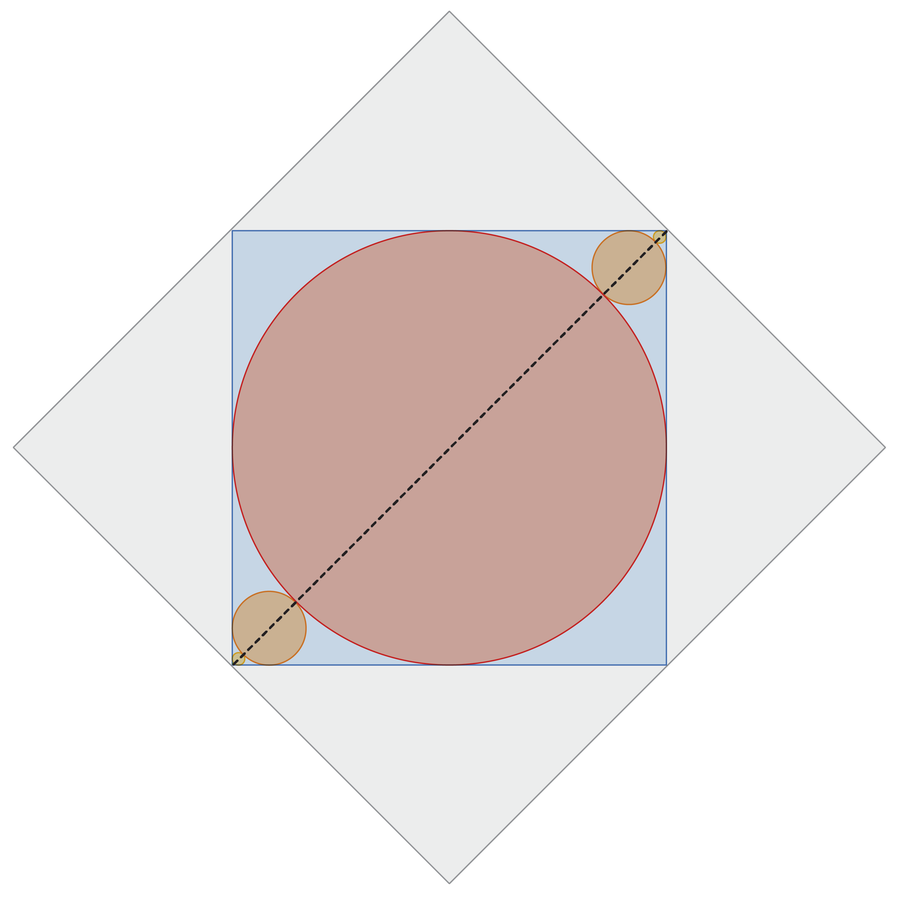
نظرًا لأن عدد لا نهائي من الدوائر تتجه نحو زوايا المربع الأزرق، فإن مجموع أقطار الدوائر يساوي طول قطر المربع الأزرق (في الصورة كخط متقطع). هذا الطول يساوي 1 لأن المربع الرمادي الخارجي له طول ضلع 1.
نحن نحب أن نسمع منك! مراسلتنا على البريد الإلكتروني في games@sciam.com لمشاركة تجربتك.

التعليقات